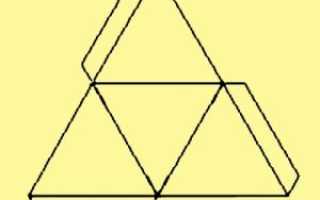
Как сделать тетраэдр из бумаги

Как из бумаги сделать тетраэдр?

Тетраэдр – самая простая фигура из многоугольников. Он состоит из четырех граней, каждая из которых представляет собой равносторонний треугольник, при этом каждая из сторон соединяется с другой всего лишь одной гранью. При изучении свойств этой трехмерной геометрической фигуры для наглядности лучше всего сделать модель тетраэдра из бумаги.

Как склеить тетраэдр из бумаги?

Для построения простого тетраэдра из бумаги нам понадобится:

собственно бумага (плотная, можно использовать картон);
транспортир;
линейка;
ножницы;
клей;
тетраэдр из бумаги, схема.

Работу над тетраэдром начинаем с рисования развертки из бумаги. Если выполнение фигуры планируется из обычной бумаги, можно чертить развертку прямо на ней.
Чертим прямую, которая будет являться гранью тетраэдра. С двух концов откладываем углы по 60 ⁰ , а через полученные точки проводим прямые линии до их пересечения. У нас получился равносторонний треугольник.
Далее на каждой стороне полученного треугольника строим такие же. От каждого конца снова откладываем по 60 ⁰ и соединяем. В результате должна получиться схема, состоящая из четырех равносторонних треугольников.
Для того, чтобы развертку можно было склеить и получить тетраэдр, следует сделать припуски по 1 см с трех сторон разных треугольников. В результате получается вот такой чертеж .
Вырезаем развертку и сгибаем ее по всем линиям, припуски загибаем внутрь, если нужно, обрезаем углы. Мажем их клеем и прижимаем ко внутренним сторонам граней, состыковав линию сгиба между стороной и припуском со стороной свободного треугольника.

Несколько дополнительных рекомендаций:

если бумага очень плотная, то по местам сгибов следует провести твердым предметом, например, ребром линейки;
для того, чтобы получить разноцветный тетраэдр, можно раскрасить грани или выполнить развертку на листах цветной бумаги.

Как из бумаги сделать тетраэдр без склеивания?

Предлагаем вашему вниманию мастер-класс, в котором рассказывается, как собрать 6 тетраэдров из бумаги в единый модуль при помощи техники оригами.

5 пар квадратных листов бумаги различных цветов;
ножницы.

Каждый лист бумаги делим на три равные части, разрезаем и получаем полосы, соотношение сторон в которых 1 к 3. В результате получаем 30 полос, из которых и будем складывать модуль.
Кладем полосу пред собой лицевой стороной вниз, вытянув по горизонтали. Сгибаем пополам, разворачиваем и подгибаем к середине края.
На дальнем правом краю сгибаем угол так, чтобы сделать стрелку, поведя ее на 2-3 см от края.
Аналогичным образом сгибаем левый угол (фото как из бумаги сделать тетраэдр 3).
Перегибаем правый верхний угол маленького треугольничка, который получился в результате предыдущей операции. Таким образом, боковые стороны сложенного края окажутся под одинаковым углом.
Разворачиваем полученную складку.
Разворачиваем левый уголок и по уже имеющимся линиям сгиба заворачиваем угол внутрь как показано на фото.
В правом углу сгибаем верхний край вниз таким образом, чтобы он пересекся со складкой, сделанной во время операции №3.
Внешний край еще раз заворачиваем направо, используя складку, выполненную в результате операции №3.

Если вы справились с тетраэдром, можно продолжить и смастерить из бумаги призму, икосаэдр, параллелепипед и другие геометрические фигуры.

Как сделать тетраэдр из бумаги: развертка для склеивания

В школе на уроке геометрии многим школьникам задают сделать тетраэдр. Иногда такое задание может вызвать недоумение. Однако, такая объемная фигура делается очень просто из бумаги, если есть пошаговая инструкция по ее изготовлению. Полезные советы по практике помогут сделать его быстро и правильно.

Что такое тетраэдр

С помощью наглядной объемной фигуры детям проще научиться иметь представление о пространственном мышлении. В этом помогут объемные геометрические фигуры, сделанные своими руками из бумаги. Тетраэдр представляет собой многоугольную фигуру, которая считается простейшей. Он состоит из 4-х граней, каждая из них является равносторонним треугольником. Стороны треугольников соединяются между собой только одной гранью. В фигуре есть также четыре вершины и шесть ребер.

Людей с давних пор привлекали многогранники как удивительные символы симметрии. Они считали их божественными фигурами. Эти фигуры очень важны в развитии математического мышления детей дошкольного и школьного возраста. Они способствуют развитию геометрического представления и пространственного мышления.

На самом деле такая фигура встречается нам повсюду. Однако, сразу ее заметить сложно. Выполненная из стержней, она встречается как основа для пространственных конструкций:

Для того чтобы получить такую фигуру, можно не прибегать к сложным математическим вычислениям. Полученная модель позволит иметь наглядное представление о свойствах геометрической фигуры в объемном изображении.

Варианты выполнения

Есть несколько способов выполнения фигуры, но лучше всего использовать самый простой и распространенный. В этом случае используется готовый шаблон, либо нужно нарисовать равносторонний треугольник. У фигуры на рисунке должны быть «лепестки», чтобы склеить их потом между собой.

При использовании собственного рисунка для склеивания есть свои преимущества. Для такой фигуры обычно берут бумагу разных цветов, что дает готовому изделию наглядный и интересный вид.

Во втором варианте применяют в склеивании не отдельные треугольники, а соединенные между собой. Такую заготовку называют разверткой тетраэдра. Лепестки находятся на всех открытых гранях треугольника либо на нескольких, для нормальной фиксации.

Более сложный способ — использование модульного варианта оригами. Для этого необходимо иметь достаточное количество бумаги, а главное — терпение и усидчивость. Поскольку такая работа кропотливая, она требует времени.

В любом из приведенных вариантов потребуется терпение и желание. В каждом из них есть свои преимущества. Выбор зависит от предназначения модели.

Необходимые материалы и инструменты

Для выполнения самого простого бумажного тетраэдра понадобятся следующие предметы:

плотная цветная бумага (желательно картон);
линейка;
ножницы;
транспортир;
клей;
инструкция (схема);
тетраэдр из бумаги.

Очень важно перед началом выполнения работы ознакомиться с инструкцией. Это позволит получить одинаковые и идентичные стороны треугольника.

Развертка тетраэдра для склеивания

Ход работы будет зависеть от используемой бумаги. Если это картон, тогда необходимо для начала нарисовать развертку на бумаге. При использовании обычной бумаги развертка чертится прямо там.

Для начала нужно начертить прямую линию, которая является гранью фигуры. С двух сторон необходимо отметить углы по 60 о . После этого полученные точки соединяются прямой линией до их пересечения. В итоге получается равносторонний треугольник.

После этого на каждой стороне полученного треугольника необходимо отложить такие же линии. Со всех концов откладываются 60 о и снова соединяются прямой линией. В итоге при правильном выполнении получается схема их 4-х равносторонних треугольников.

Для получения хорошей и удобной для склеивания развертки необходимо сделать припуски по 1 см с 3-х сторон каждого треугольника. Если все выполнено правильно, получается чертеж, как на фото.

Теперь остается аккуратно вырезать развертку, согнуть все линии, а припуски загнуть внутрь. При необходимости можно обрезать уголки. Теперь их нужно промазать клеем, стыкуя линию сгиба между стороной и припуском к стороне свободного треугольника. Припуски прижимаются к внутренним сторонам граней.

Несколько советов

При использовании плотной бумаги, например, картона в местах сгибов желательно провести линии твердым предметом. Лучше всего для этого подойдет линейка: ее ребром проводят линии.

Чтобы получить разноцветный тетраэдр лучше применять цветную бумагу или же раскрасить его грани в разные цвета.

Для изготовления тетраэдра также можно применить самоклеющуюся бумагу. В таком варианте клей не понадобится.

Видео

Посмотрите, как легко и быстро можно сделать тетраэдр из бумаги.

Тетраэдр

Древние греки дали многограннику имя по числу граней. «Тетра» означает четыре, «хедра» – означает грань (тетраэдр – четырехгранник).

Поэтому на вопрос – “что такое тетраэдр?”, можно дать следующее определение: ” Тетраэдр это геометрическое тело из четырех граней, каждая их которых – правильный треугольник “.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .

Тетраэдр имеет следующие характеристики:

Тип грани – правильный треугольник;
Число сторон у грани – 3;
Общее число граней – 4;
Число рёбер примыкающих к вершине – 3;
Общее число вершин – 4;
Общее число рёбер – 6;

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.

Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.

Отметим, что очень редко, но встречаются геометрические тела составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.

Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы тетраэдра определяется по формуле:

, где a – длина стороны .

Сфера может быть вписана внутрь тетраэдра.

Радиус вписанной сферы тетраэдра определяется по формуле:

Площадь поверхности тетраэдра

Для нагладности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:

Объем тетраэдра определяется по следующей формуле:

Высота тетраэдра определяется по следующей формуле:

Расстояние до центра основания тетраэдра определяется по формуле:

Вариант развертки

Тетраэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка – единая деталь с линиями сгибов.

Древнегреческий философ Платон ассоциировал тетраэдр с “земным” элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.

Заметим, что это не единственный вариант развертки.

Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
– если Вы предполагаете распечатать на цветном принтере – цветная развертка
– если Вы предполагаете использовать для сборки цветной картон – развертка